
Constraint Relaxation IK in 2D
 Inverse kinematics (IK) solvers often become mathematically intensive or computationally expensive with long kinematic chains or when functioning in higher dimensions. I am going to cover an approach to solving IK that is easy to understand, handles any number of joints, and is easy to implement in any dimension. We will walk through a two dimensional example and I'll present sample code to perform the algorithm.
Inverse kinematics (IK) solvers often become mathematically intensive or computationally expensive with long kinematic chains or when functioning in higher dimensions. I am going to cover an approach to solving IK that is easy to understand, handles any number of joints, and is easy to implement in any dimension. We will walk through a two dimensional example and I'll present sample code to perform the algorithm.
A basic kinematic chain of joints with no rotational constraints can be viewed as a set of points (the joint positions) with distance constraints between pairs (bones with a fixed length). By iteratively stretching the bones towards our target and resolving these distance constraints, we will converge on a solution to the system. This approach to solving the IK problem is very similar to solving constraints in a verlet based physics system (for more information on verlet physics, I recommend reading Advanced Character Physics by Thomas Jakobsen). For a sample implementation of constraint relaxation based IK, you can download the RJ_Demo_IK application.
You might also be interested in the following articles on different IK solvers:
Reaching the Target
At the end of the day, we want the root joint to remain at its initial position, the length of each joint to stay rigid, and the end effector (end of the final joint) to touch the target. The first step is to get the position of all of our joints and the target in a common space. Bones are often stored as rotations relative to a parent bone's orientation. If this is the case, we need to concatenate all of the bone transformations up to the root of the bone chain and convert our target into the same space as our joint positions.
Now that we have our joint positions in a common space, we can start the constraint relaxation process. Let's walk through an example iteration.
The root joint is located at the origin in the initial kinematic chain orientation (figure 1a).
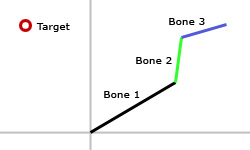
figure 1a
As our first step, we move the final joint (bone3) to be in range of the target. In other words, we place the end effector at the target position by pointing the bone towards the target and sliding is appropriately. Note that this will stretch or compress the parent. In the example, bone2 is stretched (figure 1b). We are basically, snapping the end effector to the target and then constraining the base of the end bone (bone3) to be the appropriate length from the end effector.
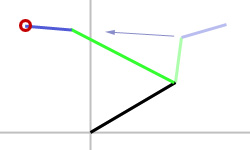
figure 1b
We now need to constrain the next bone up the chain to be the appropriate length. In our case, that means bone2 will be compressed back down to its original size (figure 1c). We can adjust the length of the bone by moving either end point. In the example, half of the modification is applied to each end (shrinking the bone towards its center). We could also have weighted each end differently to prefer modification of the child joint position or the current joint position. Weighting the relaxation process with different ratios can be used create different relaxation behavior. For example, weighting motion towards the parent bones will distribute the relaxation down the bone chain and create a smoother curve along the bones.
For a longer bone chain, this step is repeated for each bone along the chain up to and not including the root bone.
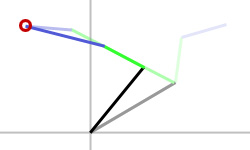
figure 1c
We can now resolve the root bone's length. In doing so, we want to leave the base of the chain at its original location. We can only modify the end connected to the first child bone (bone2). In the example, bone1 is stretched to match its original length (figure 1d).
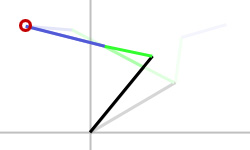
figure 1d
We now have a series of points that are a much closer representation to a solution than we started with. If we want to find an even better approximation, we can repeat multiple constraint relaxation passes along the bones. This would consist of once again constraining the end bone (figure 1b), followed by the interior bones (figure 1c), and finally the root bone (figure 1d). Once we have iterated a reasonable number of times (up to a max number or until the positions come to rest), we can apply the results back onto the bone chain.
Our relaxed joint positions are not guaranteed to be at a solution with the proper bone lengths. We may have stopped iterating before a valid solution was found, or there may have been no valid solution leaving the bones stretched. There are a number of ways to interpret the results of the relaxation. We could actually just use the stretched results if stretched bones are a valid option for the use case. We could also reconstrain the bone lengths looping from the root bone out to the end effector. In this example, I have chosen to extract the resulting angles from the single relaxation iteration result and apply them back onto the bones of appropriate length (figure 1e).
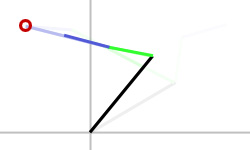
figure 1e
Due to only using a single relaxation iteration, a valid result was not found on this frame, but if your use case allows, this updated chain can be used as the initial pose on the next frame to distribute the problem over time.
Resolving Constraints
When resolving a distance constraint for a bone, we have two end points and the constrained length between them. End point \(\mathbf{b_1}\) will be base of the current bone. End point \(\mathbf{b_2}\) will be the base of the child bone. Length \(l_1\) will be the desired distance between \(\mathbf{b_1}\) and \(\mathbf{b_2}\). We will also support positive relaxation weights, \(w_1\) and \(w_2\), corresponding to the end points. The higher an endpoint is weighted, the more that endpoint will move in the solution. If an endpoint is given a zero weight, it will not move at all. If both end points are given the same weight, they will move equal distances.
As a first step, we can check the bone weights for a cases that implies we shouldn't do any work. If the total weight, \(w_1 + w_2\), is zero neither joint should move and the constraint is skipped.
Next we check if the squared distance between the end points is zero. Let \(\mathbf{v} = \mathbf{b_2}- \mathbf{b_1}\) and then use the dot product \(\mathbf{v} \cdot\mathbf{v}\) to get the squared distance. If the result is zero, it implies that the end points are directly on top of each other. This makes it a bit hard to choose the best direction for stretching the bones. We will instead skip constraints in this situation with the hope that either later in this iteration or on a following iteration the points will be stretched apart by one of the neighboring constraints being resolved.
Now that we have found a constraint to modify, we need to compare the distance between the end points with the given bone length \(l_1\). The distance between \(\mathbf{b_1}\) and \(\mathbf{b_2}\) can be calculated as \(d = \sqrt{ \mathbf{v} \cdot \mathbf{v}}\).
We need to adjust the current distance by \(l_1-d\). We can now compute a vector that would move \(\mathbf{b_2}\) the appropriate distance from \(\mathbf{b_1}\) by normalizing \(\mathbf{v}\), and rescaling it to the desired change in distance, \(l_1-d\). This gives us a new vector \(\mathbf{u} = (l_1-d)\frac{\mathbf{v}}{d}\).
Rather than directly adding \(\mathbf{u}\) to \(\mathbf{b_1}\), we want to distribute it across \(\mathbf{b_1}\) and \(\mathbf{b_2}\) based on the relaxation weights. Note that when modifying \(\mathbf{b_1}\) we will be subtracting \(\mathbf{u}\) to move the endpoint in the opposite direction.
To distribute the weighted modification across both joints, we will use the following equations.
\(\mathbf{b_1}=\mathbf{b_1}-\mathbf{u}\frac{w_1}{w_1+w_2}\)
\(\mathbf{b_2}=\mathbf{b_2}+\mathbf{u}\frac{w_2}{w_1+w_2}\)
Our joints are now at the appropriate distance and the constraint has been resolved.
Implementing for Higher Dimensions
One of the benefits to using constraint relaxation is that the algorithm barely changes when using it in higher dimensions. The constraint relaxation loop described didn't even specify a dimension for the vectors it was using. It just said when to scale, add, or use the dot product. All of these operations are easily performed on vectors of any dimension. Feel free to go crazy and solve some n-dimensional IK problem.
The only part of the algorithm that really changes when raising the dimension is the method of mapping the world space positions back onto your original bone chain. For example, if you are working in three dimensional space, your bone chain orientations are probably described with matrices or quaternions instead of the single angle used in my two dimensional example. When mapping the resulting line segments from the relaxation process back onto three dimensional joints, there are an infinite number of options. The line segment only constrains where one of the joint's axes should be pointed. The remaining two axes can be spun around the constrained axis in any way you want. One option for choosing an optimal solution is to construct a parent space orientation as close as possible to the joint's original parent space orientation before the IK was applied.
Local Minima
Constraint relaxation has a similar set of local minima to those found in CCD. From certain initial poses, the algorithm will fail to find the proper solution to a problem. Fortunately, this doesn't come up often in practice and depending on the requirements of your IK simulation and the mobility of your kinematic chain, you may never see it.
Given a two bone chain where both bones start with no rotation, we can place the target in a position that will lock up the constraint relaxation at an invalid result. Our initial setup can be seen in figure 2a.
| Initial orientation. |
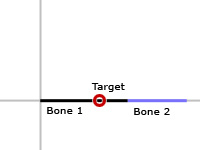 figure 2a |
If the constraint relaxation was able to give us a valid solution, bone1 would bend away from the target allowing bone2 to bend towards the target. One possible valid solution is shown in figure 2b.
| Desired solution orientation. |
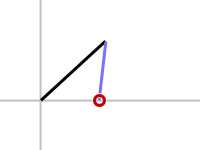 figure 2b |
When actually performing the algorithm, we will get stuck at a local minimum (see figure 2c). The first step will point bone2 towards the target. This makes bone1 and bone2 collinear. It is now bone1's turn to resolve its distance constraint which will not break the collinearity. Neither of these steps rotated bone1 away from the target and we end up in a situation where neither bone will move as we continue to iterate the algorithm.
| Resulting orientation. |
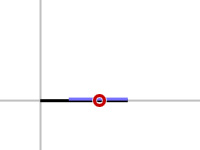 figure 2c |
The algorithm considers one joint at a time with no care about how the rest of the joints behave. The only part of the algorithm that even recognizes the joint hierarchy is the requirement that we loop backwards from the end joint to the root joint. It should also be noted that the individual steps of the algorithm aren't aware that they are part of a larger iteration towards a solution. This creates a fairly myopic view of the larger IK problem when resolving a single joint's distance constraint. I would be interested in developing a way to detect and resolve these lock ups, but am yet to require such a robust system in practice.
Writing the Code
We can now program a constraint relaxation based IK solver. The code is sourced from the RJ_Demo_IK application that can be downloaded to see a sample implementation. In RJ_Demo_IK, the bones are natively stored as pairs of parent relative angles and lengths. Because of this, the code is broken down into a three step process. An initial function is used to convert from the native bone layout to the world space positions used by the constraint relaxation process. This is followed by a function that performs a single iteration of constraint relaxation. This function is called multiple times depending on the desired number of iterations. A final function is used to convert back to the RJ_Demo_IK native format.
These code samples are released under the following license.
/******************************************************************************
Copyright (c) 2008-2009 Ryan Juckett
http://www.ryanjuckett.com/
This software is provided 'as-is', without any express or implied
warranty. In no event will the authors be held liable for any damages
arising from the use of this software.
Permission is granted to anyone to use this software for any purpose,
including commercial applications, and to alter it and redistribute it
freely, subject to the following restrictions:
1. The origin of this software must not be misrepresented; you must not
claim that you wrote the original software. If you use this software
in a product, an acknowledgment in the product documentation would be
appreciated but is not required.
2. Altered source versions must be plainly marked as such, and must not be
misrepresented as being the original software.
3. This notice may not be removed or altered from any source
distribution.
******************************************************************************/
When working with two dimensional rotations, it is often useful to wrap angles outside of the \([-\pi,\pi]\) range back into the \([-\pi,\pi]\) range. The constraint relaxation functions make use of this helper function.
///***************************************************************************************
/// SimplifyAngle
/// This function will convert an angle to the equivalent rotation in the range [-pi,pi]
///***************************************************************************************
private static double SimplifyAngle(double angle)
{
angle = angle % (2.0 * Math.PI);
if( angle < -Math.PI )
angle += (2.0 * Math.PI);
else if( angle > Math.PI )
angle -= (2.0 * Math.PI);
return angle;
}
This class is used to represent the local space bones used natively by the application.
///***************************************************************************************
/// Bone_2D_ConstraintRelaxation
/// This class is used to supply the constraint relaxation functions with a bone's
/// representation relative to its parent in the kinematic chain.
///***************************************************************************************
public class Bone_2D_ConstraintRelaxation
{
public double angle; // angle in parent space
public double length; // length of the bone (relaxation constraint)
public double weight; // weight of the bone during relaxation
};
This class is used to represent the world space bones used by the constraint relaxation.
///***************************************************************************************
/// Bone_2D_ConstraintRelaxation_World
/// This class is used to supply the constraint relaxation functions with a bone's
/// representation in world space.
///***************************************************************************************
public class Bone_2D_ConstraintRelaxation_World
{
public double x; // x position in world space
public double y; // y position in world space
public double length; // length of the bone (relaxation constraint)
public double weight; // weight of the bone during relaxation
};
At the start of each update, the application uses this function to convert its local space bones into world space bones that the constraint relaxation algorithm can process.
///***************************************************************************************
/// CalcIK_2D_ConstraintRelaxation_ConvertToWorld
/// This is a helper function to generate a world space bone chain for relaxation given
/// a local space bone chain.
///***************************************************************************************
public static void CalcIK_2D_ConstraintRelaxation_ConvertToWorld
(
out List<Bone_2D_ConstraintRelaxation_World> worldBones, // Output world space bones
List<Bone_2D_ConstraintRelaxation> localBones // Input local space bones
)
{
int numBones = localBones.Count;
Debug.Assert(numBones > 0);
// create the list to output
worldBones = new List<Bone_2D_ConstraintRelaxation_World>();
// Start with the root bone.
Bone_2D_ConstraintRelaxation_World rootWorldBone
= new Bone_2D_ConstraintRelaxation_World();
rootWorldBone.x = 0;
rootWorldBone.y = 0;
rootWorldBone.length = localBones[0].length;
rootWorldBone.weight = localBones[0].weight;
worldBones.Add( rootWorldBone );
double prevAngle = localBones[0].angle;
double prevAngleCos = Math.Cos( prevAngle );
double prevAngleSin = Math.Sin( prevAngle );
// Convert child bones to world space.
for( int boneIdx = 1; boneIdx < numBones; ++boneIdx )
{
Bone_2D_ConstraintRelaxation_World prevWorldBone = worldBones[boneIdx-1];
Bone_2D_ConstraintRelaxation prevLocalBone = localBones[boneIdx-1];
Bone_2D_ConstraintRelaxation_World newWorldBone
= new Bone_2D_ConstraintRelaxation_World();
newWorldBone.x = prevWorldBone.x + prevAngleCos*prevLocalBone.length;
newWorldBone.y = prevWorldBone.y + prevAngleSin*prevLocalBone.length;
newWorldBone.length = localBones[boneIdx].length;
newWorldBone.weight = localBones[boneIdx].weight;
worldBones.Add(newWorldBone);
prevAngle = prevAngle + localBones[boneIdx].angle;
prevAngleCos = Math.Cos( prevAngle );
prevAngleSin = Math.Sin( prevAngle );
}
}
This function is called in a loop to update the world space bones. Each call brings the bones closer to a valid solution.
///***************************************************************************************
/// CalcIK_2D_ConstraintRelaxation
/// Given a bone chain located at the origin, this function will perform a single
/// relaxation iteration. This finds a solution of bone angles that places the final bone
/// in the given chain at a target position. The supplied bone angles are used to prime
/// the iteration. If a valid solution does not exist, the angles will move as close to
/// the target as possible. The user should resupply the updated angles until a valid
/// solution is found (or until an iteration limit is met).
///***************************************************************************************
public static void CalcIK_2D_ConstraintRelaxation
(
ref List<Bone_2D_ConstraintRelaxation_World> bones, // Bone values to update
double targetX, // Target x position for the end effector
double targetY // Target y position for the end effector
)
{
// Set an epsilon value to prevent division by small numbers.
const double epsilon = 0.0001;
int numBones = bones.Count;
Debug.Assert(numBones > 0);
//===
// Constrain the end bone to the target.
{
int boneIdx = numBones-1;
double toTargetX = targetX - bones[boneIdx].x;
double toTargetY = targetY - bones[boneIdx].y;
double toTargetLenSqr = toTargetX*toTargetX + toTargetY*toTargetY;
if( toTargetLenSqr > epsilon )
{
double toTargetLen = Math.Sqrt(toTargetLenSqr);
double toTargetScale = (bones[boneIdx].length/toTargetLen) - 1.0;
bones[boneIdx].x -= toTargetScale*toTargetX;
bones[boneIdx].y -= toTargetScale*toTargetY;
}
}
//===
// Perform relaxation on the bones in a loop from the final bone to the first child
// bone.
for( int boneIdx = numBones-2; boneIdx >= 1; --boneIdx )
{
Bone_2D_ConstraintRelaxation_World curBone = bones[boneIdx];
Bone_2D_ConstraintRelaxation_World childBone = bones[boneIdx+1];
// Get the vector from the current bone to the child bone.
double toChildX = childBone.x - curBone.x;
double toChildY = childBone.y - curBone.y;
double toChildLenSqr = toChildX*toChildX + toChildY*toChildY;
double totalWeight = curBone.weight + childBone.weight;
if( toChildLenSqr > epsilon && totalWeight > epsilon )
{
double toChildLen = Math.Sqrt(toChildLenSqr);
double toChildScale =
((bones[boneIdx].length/toChildLen)-1.0) / totalWeight;
double curBoneScale = toChildScale * curBone.weight;
double childBoneScale = toChildScale * childBone.weight;
curBone.x -= curBoneScale * toChildX;
curBone.y -= curBoneScale * toChildY;
childBone.x += childBoneScale * toChildX;
childBone.y += childBoneScale * toChildY;
}
}
//===
// Constrain the first child joint to the root joint
if( numBones > 1 )
{
int boneIdx = 0;
// Get the vector from the current bone to the child bone.
double toChildX = bones[boneIdx+1].x - bones[boneIdx].x;
double toChildY = bones[boneIdx+1].y - bones[boneIdx].y;
double toChildLenSqr = toChildX*toChildX + toChildY*toChildY;
if( toChildLenSqr > epsilon )
{
double toChildLen = Math.Sqrt(toChildLenSqr);
double toChildScale = (bones[boneIdx].length/toChildLen) - 1.0;
bones[boneIdx+1].x += toChildScale * toChildX;
bones[boneIdx+1].y += toChildScale * toChildY;
}
}
}
After enough iterations have been performed, the following function is used to convert the bones back to the local space format native to the application.
///***************************************************************************************
/// CalcIK_2D_ConstraintRelaxation_ConvertToLocal
/// This is a helper function to update a local space bone chain after relaxation has been
/// performed on the corresponding world space bone chain.
///***************************************************************************************
public static void CalcIK_2D_ConstraintRelaxation_ConvertToLocal
(
ref List<Bone_2D_ConstraintRelaxation> localBones, // Update local space bones
List<Bone_2D_ConstraintRelaxation_World> worldBones, // Input world space bones
double targetX, // Target x position for the end effector
double targetY // Target y position for the end effector
)
{
Debug.Assert(localBones.Count == worldBones.Count);
int numBones = localBones.Count;
Debug.Assert(numBones > 0);
// Extract bone angles for all bones but the end bone
double prevWorldAngle = 0.0;
for( int boneIdx = 0; boneIdx < numBones-1; ++boneIdx )
{
double toNextBoneX = worldBones[boneIdx+1].x - worldBones[boneIdx].x;
double toNextBoneY = worldBones[boneIdx+1].y - worldBones[boneIdx].y;
double worldAngle = Math.Atan2(toNextBoneY,toNextBoneX);
double newAngle = SimplifyAngle(worldAngle - prevWorldAngle);
localBones[boneIdx].angle = newAngle;
prevWorldAngle = worldAngle;
}
// Point the end bone towards the target
{
int boneIdx = numBones-1;
double toTargetX = targetX - worldBones[boneIdx].x;
double toTargetY = targetY - worldBones[boneIdx].y;
double worldAngle = Math.Atan2(toTargetY,toTargetX);
double newAngle = SimplifyAngle(worldAngle - prevWorldAngle);
localBones[boneIdx].angle = newAngle;
}
}
Comments